The possum and the cucumber: Where are we on the wellbeing scale?

I recently saw the following image macro on Facebook.

This raises an interesting question in the philosophy of wellbeing. Opossums are (plausibly) prudential subejcts: things can go well for an opossum, or poorly for her. Opossums have mental states—they can experience (dis)pleasure and have preferences—, and, if humans have a telos, so (perhaps) do opies. (It would be a peculiar datum indeed that there be human-relevant prudential properties without this being so of similar enough beings.)

Cucumbers, on the other hand, are not prudential subjects. Nothing can go well for a cucumber, and they cannot be harmed. They have no desires or phenomenal states or proper function. They are cucumbers.

When things are going well for a subject, her wellbeing is high; when things go poorly, it is low. We might think that how good things are for a subject depends in part on that subject's relevant capacities; no capacity to desire—no desires—no satisfaction thereof. We might then think that, all else equal, things are better for a human than an opossum, since, e.g., humans (perhaps!—opies are clever) have richer mental lives.

The upshot of this view for the cucumber (or any other nonsubject) is that they 'have' a wellbeing level of zero: no prudential capacities, no desires nor preferences to be satisfied or frustrated, nor pleasure nor pain nor knowledge nor friendship nor spirituality.

You might think that to suggest that cucumbers 'have' a level of wellbeing at all is a total nonsense, like speculating as to what rocks dream about. But there are two ways to have null content in your dreams: to dream not about anything, and not to dream. Similarly, when we assign a level of wellbeing zero, this can either be because things are going, on balance, neutrally for a subject, or because there is no subject for things to go well or badly for.

These capacity limit cases, or quasi-wellbeing levels, allow us to compare nonsubjects with subjects by saying, e.g., 'were this cucumber a prudential subject, its level of wellbeing would be zero', and, thus, to assert with J. S. Mill that it's better to be Socrates than a pig—and better a pig than a cucumber!

This raises the question latent in that image macro: is it really better to be an opossum than a cucumber?

The trouble with just saying 'yes' is this: we don't know where zero is; we don't know how good it is to be a cucumber—or what rocks dream about. But there's a sense in which we know exactly how good it is to be a cucumber—we know by stipulation; being a cucumber is zero. We just don't know where this stands in relation to us. Or, to put it another way, we don't know where we are (in relation to the fixed points on the scale); we don't know how good it us to be us.

But what is the upshot of this? We'll briefly consider two.

First off, let's consider (20th/21st c. value theorist) Derek Parfit's repugnant conclusion argument. Imagine you have a population A of some arbitrary size; add up all the wellbeing levels of all the people in A to get A's total wellbeing. Now, imagine a population B whose average wellbeing is slightly lower than that of A, but has enough extra people to make the sum of B-people wellbeing, B's total wellbeing, greater than that of A. So B is better than A. But we can imagine a population C that stands to B as B does to A, and a population D that stands to C as C to B, ..., and a population Z which stands to Y as Y to X, and so must be better than A. But everyone in Z has a very low—positive but tiny—level of wellbeing; they are just above zero. So, the thought goes, we should give up total wellbeing as a measure of the wellbeing of a population (since A is better than Z).

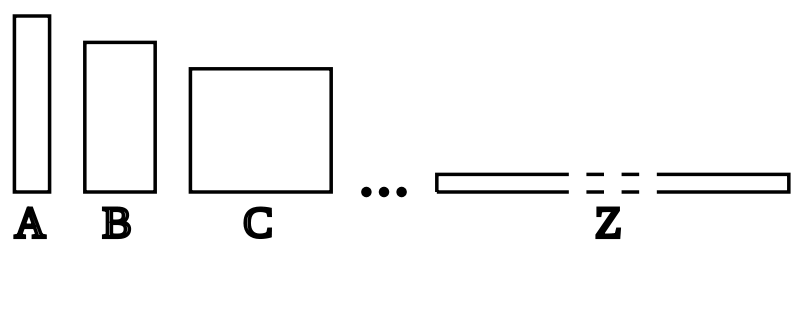
It's often implicitly assumed by people that make this argument that we are like the people in population A, but perhaps we are more like the people in Z: perhaps we are not so far above zero than we thought.

Another place the question about where we are in relation to zero raises a problem is questions concerning wellbeing and death. Some arguments for the badness of death (deprivation and comparative accounts) make implicit or explicit reference to dying or being dead having a prudential value of zero, and one's relation to zero.

(Plato's) Socrates, in the Apology, suggests that death as permanent unconsciousness would not be a harm (perhaps—the purpose of this passage is unclear). Even the immensely prudentially well-off Great King, he says, would be unable to find any experience as blissful. Anyone who has taken an midafternoon nap can see the intuitive force of this claim.

George Rudebusch (a contemporary philosopher) analyses this in terms of (20th c. ordinary language philosopher) Gilbert Ryle's distinction between sensate and modal pleasures. Consider the example of the pleasure given by listening to music. There may be some pointed and particular moments of sensate pleasure—an exquisite harmony, an unexpected leap in the melody, an inexplicably catchy hook—but even when these are absent, we are still taking some sort of pleasure from listening to the music, modal pleasure. Were I to ask you whether you enjoyed the piece, you would say 'yes', not 'I enjoyed the piece at these particular times'; you enjoyed the whole piece.

This modal sense is that in which permanent unconsciousness is endless bliss: there is no particular moment at which you take pleasure from your napping—you are asleep—; rather, you enjoy the whole nap, as Socrates enjoys the interminable peace of permanent unconsciousness. (Ryle's golfer takes pleasure in that hole-in-one on hole six, but she also takes pleasure in the whole game.)

If lack of sensation—and, suppose, (dis)pleasure, preference satisfaction/frustration, &c.—is inflected with modal pleasure, what are we to say about 'zero'? Perhaps cucumbers wallow in inexpressible bliss, and colourless green ideas sleep furiously after all.

So, we don't know where we are in relation to zero, and this throws some spanners in some elegant philosophical machines. How to resolve these issues is not altogether clear. As Shakespeare could've said: that is the question, whether 'tis nobler in the mind to suffer the slings and arrows of outrageous fortune, or to take arms against a sea of troubles, and by opposing become a cucumber.

Łukasiewicz notation on the web: a proposal

Łukasiewicz developed his prefix system of logical notation (also called 'Polish' or 'normal Polish' notation) in the 1920s as an alternative to the infix notation which arose from mathematical notation, Russell & Whitehead's Principa Mathematica, and other sources. The main advantage of his system over infix or Russellian notation was its absence of parenthesis, required by the latter to avoid ambiguity in the scope of operators.

For instance, we represent the unwieldy infix \(\neg ((p\leftrightarrow (q\land r))\to(p\lor r))\) as NCEpKqrApr.

For contemporary people interested in using logical notation, the more pressing problem with Russellian notation is that it is difficult to represent using a computer, and, unless using a typesetting engine like \(\LaTeX{}\), it almost invariably looks bad. Outside of a formal context, it is extremely inconvenient to use Russellian notation on a computer, especially on the web – though FB Messenger and other platforms now support the necessary LaTeX rendering via software like MathJax, it's awkward to write. Łukasiewicz is better, but it's difficult for most people to remember the right symbols since they're derived from Polish. Hence a different schema, more closely related to Russellian notation.

One logician frustrated by the inconvenience of infix notation.

In the table below, compare each operation's (named informally) representation in infix notation (in LaTeX mathmode and plain text) with classical Łukasiewicz notation and my proposed scheme.

Truthfunctional propositional operators

Operation	Infix (LaTeX)	Infix (plain)	Łukasiewicz	Proposal
Not	\(\neg p\) or \(\sim\! p\)	¬p or ~p	Np	¬p or ~p
Or	\(p\lor q\)	pvq	Apq	+pq
And	\(p\land q\) or \(p\cdot q\) &c.	p&q or p.q &c.	Kpq	&pq or *pq
Implies	\(p\to q\) or \(p\supset q\)	p→q	Cpq	?pq
Iff	\(p\leftrightarrow q\)	p↔q	Epq	=pq

Quantifiers

Operation	Infix (LaTeX)	Infix (plain)	Łukasiewicz	Proposal
All	\(\forall x(Fx)\) or \((x)(Fx)\)	(x)(Fx) or ∀x(Fx)	ΠxFx	*xFx
Some	\(\exists x(Fx)\)	∃x(Fx)	ΣxFx	+xFx

Modal operators

Operation	Infix (LaTeX)	Infix (plain)	Łukasiewicz	Proposal
Strong	\(\Box p\)	□p	Lp	See below
Weak	\(\Diamond p\)	◇p	Mp	See below

Please note that my proposal is not that people should give up Russellian notation globally – in an academic context, for instance, or anywhere the notation should be pretty (here one has no option but to use LaTeX). It is rather that in informal contexts where the use of rendering software is unwarranted (e.g. email and social media discussion), Russellian notation is inappropriate, and we should use more user-friendly notation instead.

One of the advantages of the proposed notation is that it is consistent with the conventions for Russellian notation: p, q, r, ... are propositions; x, y, z, ... are object variables; &c. Majuscule romans are not taken up as logical operators.

Rationale for symbol choice

Not: ¬p or ~p: these are easy to type, especially '~'. One can even maintain the distinction between '~' for classical negation and '¬' for, e.g., intuitionistic negation.

Or: +pq: disjunction is logical sum, like addition is numerical sum.

And: &pq or *pq: the ampersand is a symbol for 'and' ('et'); conjunction is logical product, like multiplication is numerical product.

Implies: ?pq: this is maybe the strangest choice. It comes from the ternay ?: operator in programming: 'a?b:c' means roughly 'if a, then return b; else return c' (we just drop the third term). We can also think of ?pq thus: 'is p the case? then q is.'

Iff: =pq: here p and q have the same truth-value (in Fregean terms, they have the same extension – denote the same thing).

All: *xFx: universal quantification works like conjunction: *xFx iff *Fa*Fb*Fc... Some logicians write \(\bigwedge x(Fx)\)

Some: +xFx: existential quantification works like disjunction: +xFx iff +Fa+Fb+Fc... Some logicians write \(\bigvee x(Fx)\)

The modal operators

The standard notation for the modal operators is \(\Box p\ \Diamond p\), but there a few alternatives – Gödel even used N (for 'necessarily') for the strong operator. One can safely adopt Łukasiewicz's Lp and Mp, but this means they can't be used for predicates &c. I have seen []p <>p, approximating the box and diamond; these are an option, but aren't great either. A hesitant suggestion would be to drop the second character of the operator: [p <p. Here one also has the option of explicitly marking the end of the operator scope as 'syntactic sugar' (like removing the outermost parenthesis in Russellian notaion). E.g., LKpq becomes [*pq or [*pq]; MKpq becomes <*pq or <*pq>.
(This is even extendable to other modalities, where [ and < are taken for logical necessity and possibility – we can have {p or {p}, (p or (p), &c.)

Figleafing and informal \(\omega\)-inconsistency

content warning: racism.

Liam Kofi Bright identified an interesting informal fallacy a couple of years ago he called 'informal omega-inconsistency'. In committing this fallacy, the speaker claims that there are things satisfying a certain property \(\phi\) but consistently denies that particular members of the domain satisfy \(\phi\). An example he gives is the speaker claiming that there are bad drivers in Pennsylvania, but denyies that any particular case of putative bad driving in Pennsylvania you present to them is down to a bad driver.

Until the speaker exhausts the domain (claims \(\neg\phi x\), for all \(x\in D\)), they are not inconsistent. The fallaciousness comes not from actual inconsistency but a sort of potent inconsistency: from its being 'apparent that this is a matter of policy, that this is how the person always responds to apparent instances of the general claim being made' (Bright). (We can think of it in terms of the conditional if the speaker were to evaluate \(\phi x\in D\), she would claim it's false.)

I want to highlight an interesting way of committing this fallacy. In the case of informal \(\omega\)-inconsistency, the reasoner prototypically wants to assent to an existential claim without assenting to what it entails (that some particular member of the domain satisfies the property): \[\not\omega_\Sigma := \exists x.\phi x.\land\neg\phi d_1\land\neg\phi d_2\land\neg\phi d_3\land\ldots\]

But one can also commit this fallacy by seeking to deny a universal claim without assenting to the presence of counterexamples to it:\[\not\omega_\Pi := \neg\forall x.\phi x.\land\phi d_1\land\phi d_2\land\phi d_3\land\ldots\]

Due to quantifier interdefinition the two formulations are biconditional,¹ but they have distinct rhetorical characters. A particularly interesting example of \(\not\omega_\Pi\)² comes from Donald Trump's infamous remark about immigrants to Usonia from Mexico:

When Mexico sends its people, they're not sending their best ... They’re bringing drugs. They’re bringing crime. They’re rapists. And some, I assume, are good people.

Trump assigns to Mexican immigrants the property \(\psi\) of bringing drugs or bringing crime or being a rapist. The absence of a quantifier raises ambiguity – in isolation, we'd normally take this to be claiming that all Mexican immigrants satisfy \(\psi\). But he then claims 'and some, I assume, are good people' – so \(\exists x.\neg\psi x\), which is flatly inconsistent with \(\forall x.\psi x\). Trump thus implies that \(\neg\forall x.\psi x\) but generally \(\psi x\). (This is equivalent to \(\not\omega_\Sigma\) with respect to \(\neg\psi\) on the same domain.)

Presumably, for each particular \(x\in D\), he would assent to \(\psi x\). He would then meet our conditional test for \(\not\omega_\Pi\), here if the speaker were to evaluate \(\psi x\in D\), she would claim it's true. So here Trump commits the fallacy of informal \(\omega\)-inconsistency in its universal form.

Jenny Saul has analysed the sort of remarks above in terms of figleafing, a device by which the speaker supplements otherwise overtly racist (&c.) remarks with a remark which raises ambiguity, doubt, and/or ensures plausible deniability (a 'figleaf', which only just covers the racism). One of the simplest (and least effective) examples is 'I'm not racist, but ...'.

Nigel Farage on BBC claiming he isn't racist, but ...

The Trump example above is a highly sophisticated one. Trump isn't merely supplementing overtly racist remarks with the claim that he isn't racist (or something meant to imply it), but is implicitly denying the racist claim he at first seems to be making (that Mexican immigrants (qua Mexican immigrants) all satisfy \(\psi\)). The figleafing is being deployed at the logical level – it is integrated in the very claims it seeks to cover.

Informal \(\omega\)-inconsistency, then, can constitute a very sophisticated figleaf by allowing the speaker to in effect appear to have it both ways. They can make a claim³ without really having to assent to it. (In the Trump case he claims that \(\neg\forall x.\psi x\) but isn't bound by its implication that there's some particular \(x\in D\) which doesn't satisfy \(\psi\).)

An interesting connexion Bright notes is to the 'no true Scotman' fallacy: (\(\not\omega_\Sigma\)) of course there are Scots who might commit brutal murders as the English do, (but Nicola Sturgeon, Carol Ann Duffy, ... wouldn't)

Notes

1. Demonstration left as an exercise!
2. Bright's example of \(\not\omega_\Sigma\) is racism (do read his blog post).
3. In \(\not\omega_\Sigma\) an existential claim; in \(\not\omega_\Pi\) a universal one.